We consider the problem of learning to choose from a given set of objects, where each object is represented by a feature vector. Traditional approaches in choice modelling are mainly based on learning a latent, real-valued utility function, thereby inducing a linear order on choice alternatives. While this approach is suitable for discrete (top-1) choices, it is not straightforward how to use it for subset choices. Instead of mapping choice alternatives to the real number line, we propose to embed them into a higher-dimensional utility space, in which we identify choice sets with Pareto-optimal points. To this end, we propose a learning algorithm that minimizes a differentiable loss function suitable for this task. We demonstrate the feasibility of learning a Pareto-embedding on a suite of benchmark datasets.

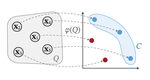
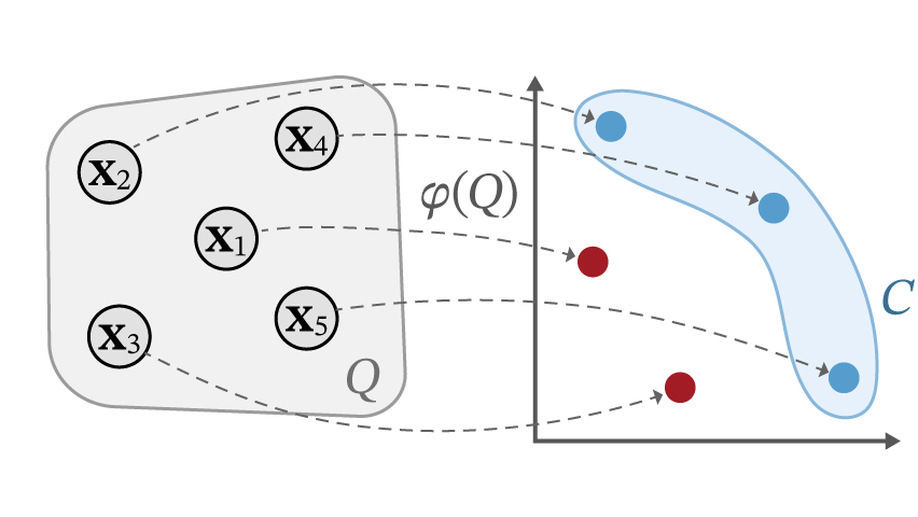
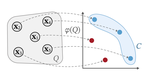
We study the problem of learning choice functions, which play an important role in various domains of application, most notably in the field of economics. Formally, a choice function is a mapping from sets to sets: Given a set of choice alternatives as input, a choice function identifies a subset of most preferred elements. Learning choice functions from suitable training data comes with a number of challenges. For example, the sets provided as input and the subsets produced as output can be of any size. Moreover, since the order in which alternatives are presented is irrelevant, a choice function should be symmetric. Perhaps most importantly, choice functions are naturally context-dependent, in the sense that the preference in favor of an alternative may depend on what other options are available. We formalize the problem of learning choice functions and present two general approaches based on two representations of context-dependent utility functions. Both approaches are instantiated by means of appropriate neural network architectures, and their performance is demonstrated on suitable benchmark tasks.

Object ranking is an important problem in the realm of preference learning. On the basis of training data in the form of a set of rankings of objects, which are typically represented as feature vectors, the goal is to learn a ranking function that predicts a linear order of any new set of objects. Current approaches commonly focus on ranking by scoring, i.e., on learning an underlying latent utility function that seeks to capture the inherent utility of each object. These approaches, however, are not able to take possible effects of context-dependence into account, where context-dependence means that the utility or usefulness of an object may also depend on what other objects are available as alternatives. In this paper, we formalize the problem of context-dependent ranking and present two general approaches based on two natural representations of context-dependent ranking functions. Both approaches are instantiated by means of appropriate neural network architectures, which are evaluated on suitable benchmark task.